A fent nevezett egyenlet a párolgásra állapít meg egy összefüggést, amelyet az agrometeorlógiában elég gyakran emlegetnek. Az egyenletnek több levezetése is ismert, mi most a fluxus gradiensének segítségével próbáljuk elõvarázsolni az összefüggést a párolgásra. Magyarán és közérthetõen, az egyenlet arra ad választ, hogy mennyi víz párolog el a növényzettel benõtt felszínrõl.
Pár fogalom: adiabatikusnak nevezzük azokat a folyamatokat, amelyek esetében a vizsgált levegõrész a környezetébõl nem vesz fel hõt és nem is ad le. A nem adiabatikus esetben van hõcsere a levegõ rész és a környezete között. A nedves hõmérséklet, az a legalacsonyabb hõmérséklet, amelyre a levegõ lehûl adott nyomáson víz elpárologtatása során. Az e jelöli a gõznyomást (páranyomást) ami a vízgõz adott térfogatrészben lévõ nyomását jelenti, es pedig a telítési gõznyomást.
A nedves felszínrõl elpárolgó nedvesség mennyiségét a szenzibilis illetve látens hõáram segítségével tudjuk kiszámolni. A szenzibilis hõáram egyenes arányban függeni fog a talaj(T0) és a levegõ(T) közötti hõmérséklet különbségtõl illetve fordított arányban a szenzibilis hõszállítási együtthatótól(rH). A hõáramot - azaz a fluxust - a következõ formulával lehet meghatározni:

A negatív elõjel annyit jelent, hogy az érték a talajtól távolodva nõ. A látens hõáram ugyancsak függeni fog a talaj hõmérsékletétõl, a szenzibilis hõszállítási együtthatótól és a gõznyomástól.
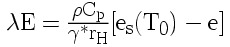
Lambda a párolgási látens hõmennyiség,amelyet konstansnak szoktak venni, a *-os változó pedig a csillagnélküli változó (azaz a gamma, amit psychrometrikus állandónak neveznek) megszorozva a pára szállítási együttható és a szenzibilis hõáram együttható arányával:
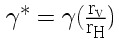
Valahogy ki kellene fejteni az egyenletben található gõznyomást, de sajnos a talaj hõmérsékletét nem ismerjük. Ezt azonban ki tudjuk számolni a psychrometrikus közelítés segítségével, azaz feltételeznünk kell hogy a talajhõmérséklet egyenlõ a nedves hõmérséklettel (T0 = Tn, ahol Tn a nedves hõmérséklet, de ezt a közelítést nem használhatjuk nagyon száraz levegõ esetén).Ebben az esetben, ha felhasználjuk a telítési páranyomásra kiszámítására vonatkozó
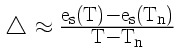
egyenletet (ahol delta a telítési gõznyomás
görbéjének meredekségét jelenti) és a psychrometrikus közelítéssel kapott T0 = Tn egyenlõséget behelyettesítjük, akkor a következõ formulához jutunk:
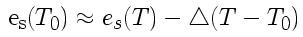
Ezt most visszahelyettesítjük a látens hõáram képletébe:
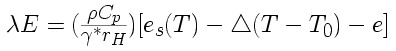
Azonban milyen kellemes meglepetés, hogy az egyenletben szereplõ levegõhõmérséklet és talajhõmérséklet különbsége a szenzibilis hõáram függvénye. Felhasználva a szenzibilis hõáram egyenletét a mostani összefüggés így írható:
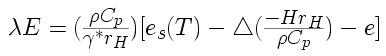
Ezt átrendezve:
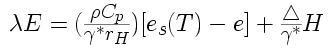
Itt most megint egy feltételezéssel kell élnünk: feltesszük, hogy nem-adiabatikus rendszert vizsgálunk. Ebben az esetben a külsõ energia fluxus - azaz a nettó sugárzás - a szenzibilis és a látens hõáram összegével lesz egyenlõ,azaz a szenzibilis hõáram így írható:
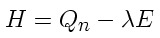
Ezt felhasználva :
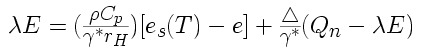
egyenletet kapjuk. Átrendezés után a következõ összefüggéssel állunk szemben:
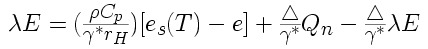
Egy kis matematikai ügyeskedés és tulajdonképpen meg is kaptuk a kívánt egyenletet:
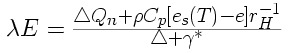
Milyen szép, mi? Ez a Penman-Monteith egyenlet egyik alakja. Kaptunk egy összefüggést, amely a levegõ hõmérsékletének,és a hõfluxusnak segítségével adja meg, hogy a nedves felszínrõl mekkora a párolgás. Már csak egy kérdés maradt: hogy lesz az egyenlet bal oldalán található látens hõáramból vízmennyiség? Ezt a következõ ekvivalencia adja meg: 1 W/m2 = 0.0352 mm/d.




